Kebebasan Linear

Bebas linear merupakan salah satu syarat yang harus dipenuhi oleh suatu himpunan untuk menjadi basis ruang vektor.

Dalam aljabar linear, sekelompok vektor disebut bebas linear (linearly independent) apabila masing-masing vektor tersebut tidak dapat ditulis sebagai kombinasi linear dari vektor-vektor yang lain. Sekelompok vektor yang tidak memenuhi syarat ini dinamakan bergantung linier (linearly dependent). Kita nyatakan definisinya sebagai berikut.

Definisi:

Jika $S=v_1,v_2,\dots ,v_r$ adalah himpunan vektor, maka persamaan vektor

mempunyai paling sedikti satu pemecahan, yakni

Jika ini adalah satu-satuya pemecahan, maka $S$ kita namakan himpunan bebas linear (linearly independent). Jika ada pemecahan lain, maka $S$ kita namakan himpunan tak bebas linear (linearly dependent).

Teorema:

Himpunan $S$ dengan dua vektor atau lebih adalah

1. Tak bebas linear jika dan hanya jika paling tidak satu diantara vektor $S$ dapat dnyatakan sebagai kombinasi linear dari vektor $S$ lainnya.
2. Bebas linear jika dan hanya jika tidak ada vektor $S$ yang dapat dinyatakan sebagai kombinasi linear dalam vektor $S$ lainnya.

Teorema:

1. Jika sebuah himpunan mengandung vektor nol, maka himpunan itu takbebas linear.
2. Sebuah himpunan mempunyai persis dua vektor takbebas linear jika dan hanya jika salah satu dari vektor itu adalah perkalian dari skalar lainnya.

Contoh 1:

Periksa apakah himpunan $S=\left\{\right(1,2),(2,5\left)\right\}$ bebas linear dalam ruang vektor $R^2$.

Pembahasan:

Perhatikan bahwa (1,2) bukan kelipatan skalar dari (2,5) dan begitupun sebaliknya. Dengan demikian, berdasarkan teorema di atas, maka himpunan $S$ adalah bebas linear.

Contoh 2:

Tinjaulah vektor-vektor $i=(1,0,0),j=(0,1,0)$ dan $k=(0,0,1)$ pada $R^3$. Perlihatkan bahwa himpunan vektor-vektor tersebut saling bebas linear.

Pembahasan:

Vektor-vektor tersebut saling bebas linear jika persamaan

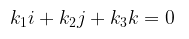
hanya dipenuhi oleh $k_1=k_2=k_3=0$ atau secara ekivalen menjadi

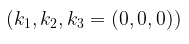
Perhatikan bahwa $k_1=0,k_2=0,k_3=0$; sehingga himpunan $S=(i,j,k)$ bebas linear. Uraian serupa dapat digunakan untuk memperlihatkan bahwa vektor-vektor $e_1=(1,0,0,\dots ,0),e_2=(0,1,0,\dots ,0),\dots ,e_n=(0,0,0,\dots ,1)$ membentuk himpunan bebas linear pada $R^n$.