Elementer
ELEMENTER
Ruang Baris, Ruang Kolom, dan Ruang Nul
Definisi
Pada Rn yang dibentuk dari baris – baris Matriks A disebut sebagai vektor baris. Sedangkan vektor – vektor.
Pada Rm yang dibentuk dari kolom – kolom matriks A disebut sebagai vektor kolom.
Definisi
Jika A adalah matrik m x n maka subruang dari Rn yang di rentang oleh vektor – vektor baris dari A disebut ruang baris dari A, dan subruang dari Rm yang direntang oleh vektor – vektor kolom dari A disebut ruang kolom dari A. Ruang solusi dari sitem persamaan yang homogen Ax = 0 yang merupakan subruang dari Rn disebut ruang null dari A.
Teorema
Jika A dan B adalah matriks – matriks yang ekuivalen baris, maka
a. Sesuatu himpunan vektor – vektor kolom dari A tertentu adalah bebas linear jika dan hanya jika vektor – vektor kolom yang bersusuaian dari B adalah bebas linear.
b. Sesuatu himpunan vektor – vektor kolom yang dari A tertentu membentuk suatu basis untuk ruang kolom dari A jika dan hanya jika vektor – vektor kolom yang bersesuaian dari B membentuk suatu basis untuk ruang kolom dari B.
Jika suatu matriks R berada dalam bentuk eselon baris, maka vektor – vektor baris dengan 1 utama membentuk suatu basis untuk ruang baris dari R dan vektor – vektor kolom dengan 1 utama dari vektor – vektor baris membentuk suatu basis untuk ruang kolom dari R.
Jika A adalah matrik sebarang, maka ruang basis dan ruang kolom dari A memiliki dimensi yang sama.
Definisi
Dimensi umum dari ruang baris dan kolom dari suatu matriks A disebut rank dari A (notasi : rank (A)), dimensi ruang nul dari A disebut sebagai nulitas dari A (notasi : nulitas (A)).
Teorema
Jika A adalah matriks dengan n kolom, maka
rank (A) + nulitas (A) = n
rank (A) = n – rank (A)
rank (A) = n – nulitas (A)
Perhatikan kolom – kolom pada matriks hasil OBE, matriks A mempunyai basis ruang kolom yaitu :
Basis ruang baris diperoleh dengan cara, mentransposkan terlebih dahalu matriks A, lakukan OBE pada A1, sehingga diperoleh:
Kolom – kolom pada hasil OBE yang memiliki satu utama bersesesuaian dengan matriks At ini berarti. Matriks A tersebut mempunyai basis ruang basis:
rank (A) = 2
nutilas (A) = n – rank(A)
= 4 – 2
= 2
Contoh :
Diberikan SPL homogen :
2p + q – 2r – 2s = 0
p – q + 2r – s = 0
-p + 2q – 4r + s = 0
3p – 3s = 0
p – 5 = 0 => p = 5
q – 2r = 0 => q = 2r
misalkan
s = a, r = b
p = a
q = 2b
Solusi SPL homogen tersebut adalah:
nutilas (A) = 2
rank (A) = 2
rank (A) + nutilas (A) = n
2 + 2 = 4
Dimensi dari basis ruang solusi dinamakan nulitas. Dengan demikian, nulitas dari SPL diatas adalah 2

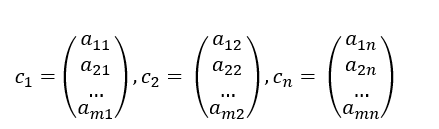







Komentar
Posting Komentar